Curvas Repulsivas – Transações ACM em Gráficos
As curvas desempenham um papel fundamental em gráficos de computador, simulação física e visualização matemática, mas a maioria das ferramentas para o projeto de curvas não faz nada para evitar cruzamentos ou auto-interseções. Este artigo desenvolve algoritmos eficientes para (auto-)repulsão de curvas planas e espaciais que se adaptam bem a problemas de projeto computacional. Nosso ponto de partida é a chamada energia do ponto tangente , que fornece uma barreira infinita à auto-interseção. Em contraste com as estratégias de detecção de colisões locais usadas, por exemplo, simulação física, essa energia considera as interações entre todos os pares de pontos e, portanto, é útil para a otimização global da forma: mínimos locais tendem a ser esteticamente agradáveis, fisicamente válidos e bem distribuídos no espaço. Uma reformulação do gradiente descendente, com base em um produto interno de Sobolev-Slobodeckij, nos permite progredir rapidamente em direção a mínimos locais – independentemente da resolução da curva. Também desenvolvemos um esquema multigrade hierárquico que reduz significativamente o custo por etapa de otimização. A energia é facilmente integrada com uma variedade de restrições e penalidades ( por exemplo ,, inextensibilidade ou prevenção de obstáculos), que usamos para aplicações que incluem empacotamento de curvas, desembaraçamento de nós, incorporação de gráficos, interpolação de spline sem cruzamento, visualização de fluxo e planejamento de caminho robótico.
|
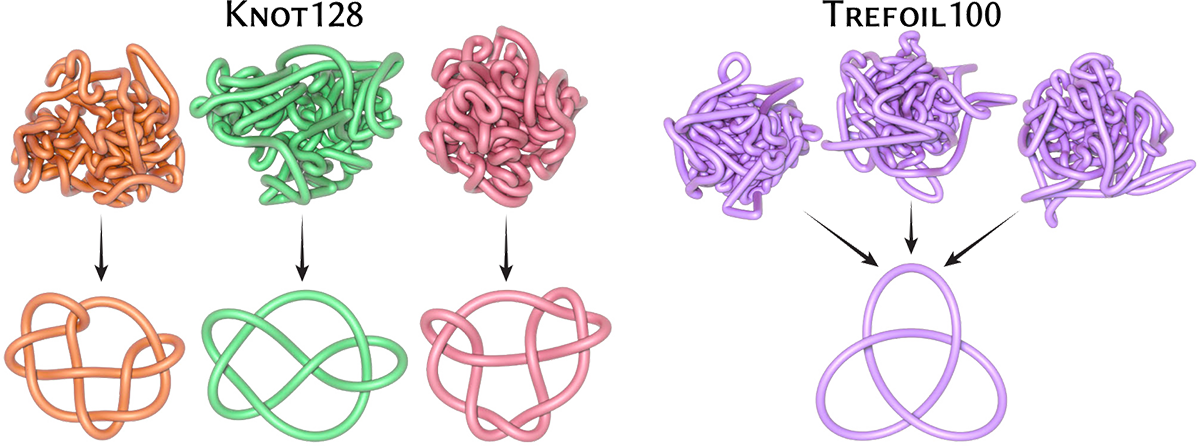
Este arquivo contém dois conjuntos de dados: Knot128 e Trefoil100 . Ambos os conjuntos de dados são “testes de estresse” para algoritmos de desembaraçamento de nós, ou seja, configurações altamente emaranhadas que podem ser difíceis de suavizar em uma incorporação de nós canônica. Knot128 é composto por nós de 128 classes de isótopos diferentes; para cada classe, fornecemos uma incorporação emaranhada e uma incorporação canônica (para referência). O Trefoil100 contém 100 encaixes emaranhados do nó do trevo . Até o momento, nenhum algoritmo – incluindo o nosso – consegue desembaraçar 100% desses nós (consulte o artigo/suplemento para estatísticas), embora cheguemos bem perto!
|
ZIP, 9,3 MB
|
repulsive-curves —Implementação C++, com visualização interativa via Polyscope . Curvas e restrições podem ser especificadas por um simples “arquivo de cena”, que é resolvido para produzir uma sequência de curvas otimizadas. As cenas suportam uma ampla variedade de restrições e objetivos, conforme descrito aqui .
Suplementar
Material Suplementar — Realizamos uma extensa comparação com 19 métodos alternativos de pré-condicionamento e otimização, descobrindo que, em geral, o esquema de Sobolev fracionado funciona significativamente melhor do que os esquemas de otimização de última geração para energias geométricas. Este documento também detalha como geramos nosso conjunto de dados de nós .
|
Este arquivo contém malhas (em várias resoluções) do unknot do artigo “Möbius Energy of Knots and Unknots” de Freedman, He e Wang, que é usado como referência de desempenho em nosso artigo.
|
ZIP, 1,8 MB
|
Figuras
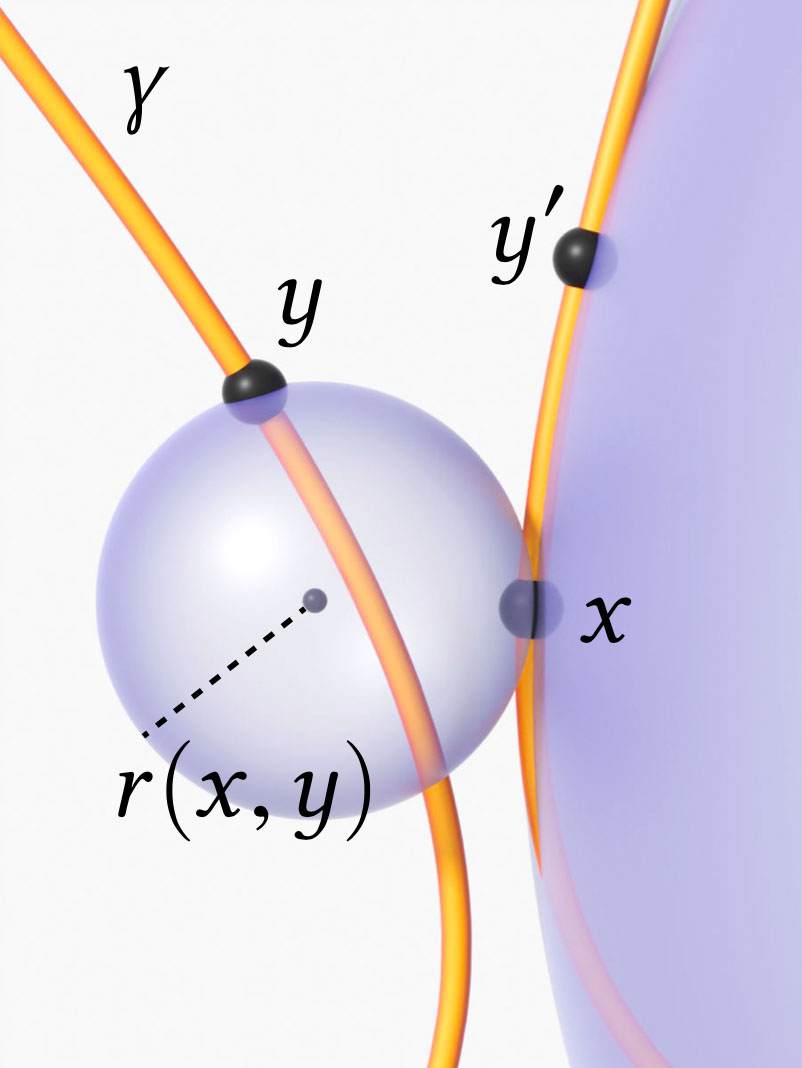
Nosso ponto de partida é a energia tangente de Buck & Orloff (1995), que para cada par de pontos x e y em uma curva considera o raio r da menor esfera tangente a x e passando por y . Ao penalizar a recíproca do raio 1/r(x,y) , a energia fornece uma barreira infinita para colisões – enquanto naturalmente ignora pontos que estão próximos no espaço simplesmente porque estão próximos ao longo da própria curva.
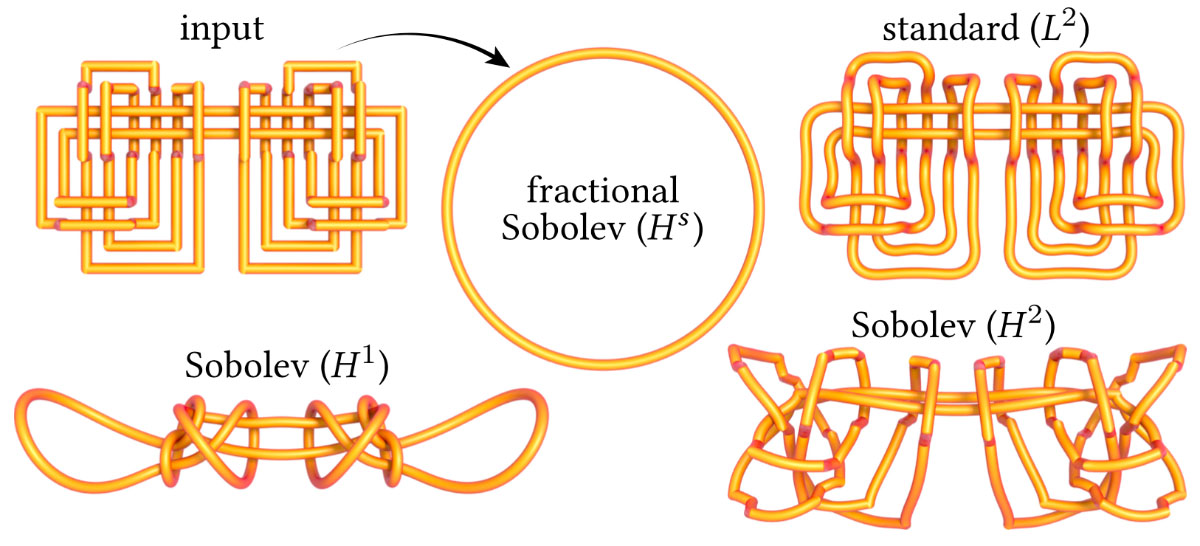
Desembaraçando o nó Freedman altamente emaranhado (canto superior esquerdo) para o círculo unitário. Para o mesmo tempo de relógio de parede, a descida de gradiente L2 padrão quase não faz progresso, enquanto a descida convencional de Sobolev falha em suavizar frequências baixas ( H 1 ) ou altas ( H 2 ). Ao combinar cuidadosamente o produto interno com a energia, nossa descida fracionária de Hs flui rapidamente para o círculo .
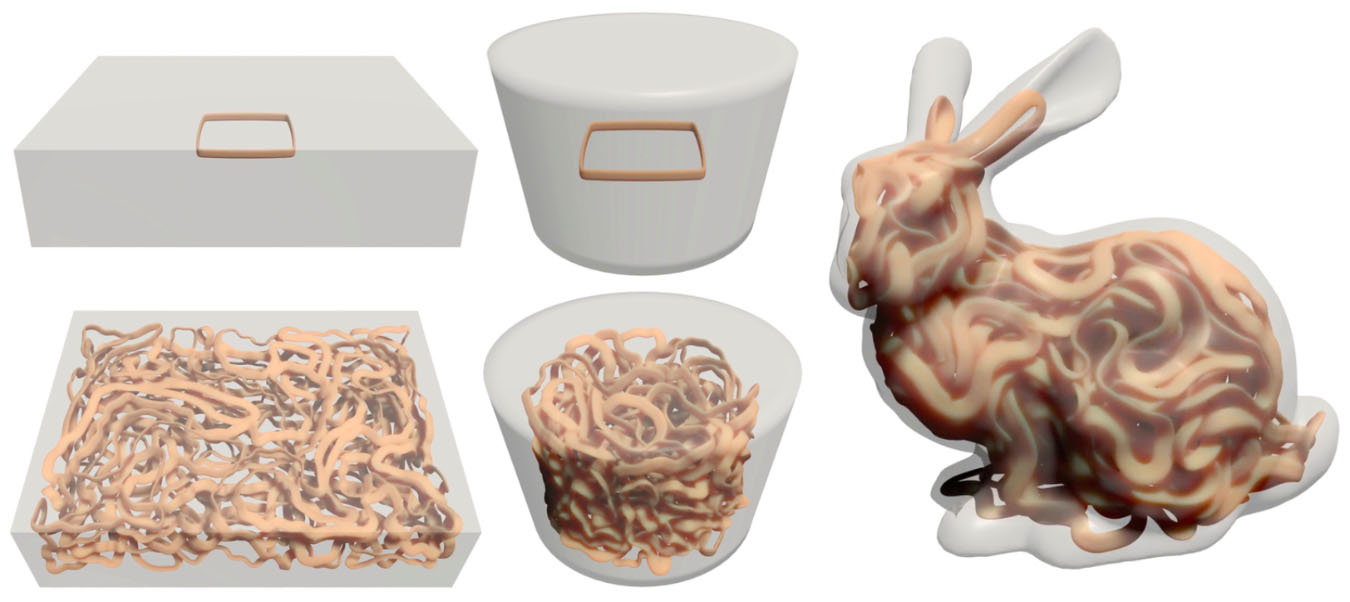
Podemos empacotar curvas em um domínio penalizando sua proximidade com seu limite e aumentando progressivamente o comprimento da aresta. (Aqui renderizamos curvas com seção transversal não circular, que não é modelada pela energia.)

Padrões obtidos restringindo uma coleção de curvas repulsivas a uma superfície e aumentando seus comprimentos (estados iniciais mostrados acima de suas configurações finais).
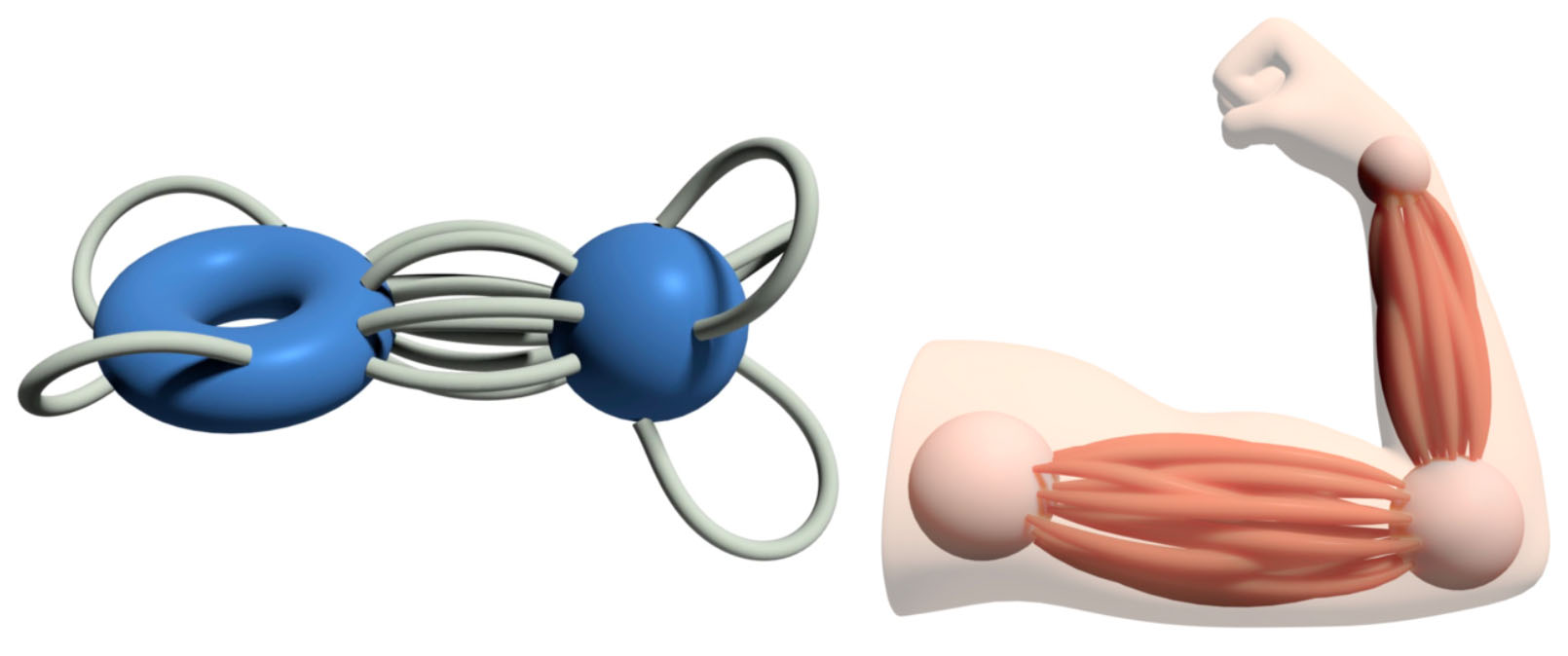
Permitir que os pontos finais da curva deslizem livremente sobre as superfícies de restrição (esquerda) permite tarefas de design, como organizar redes de músculos ou fibras musculares (direita) .
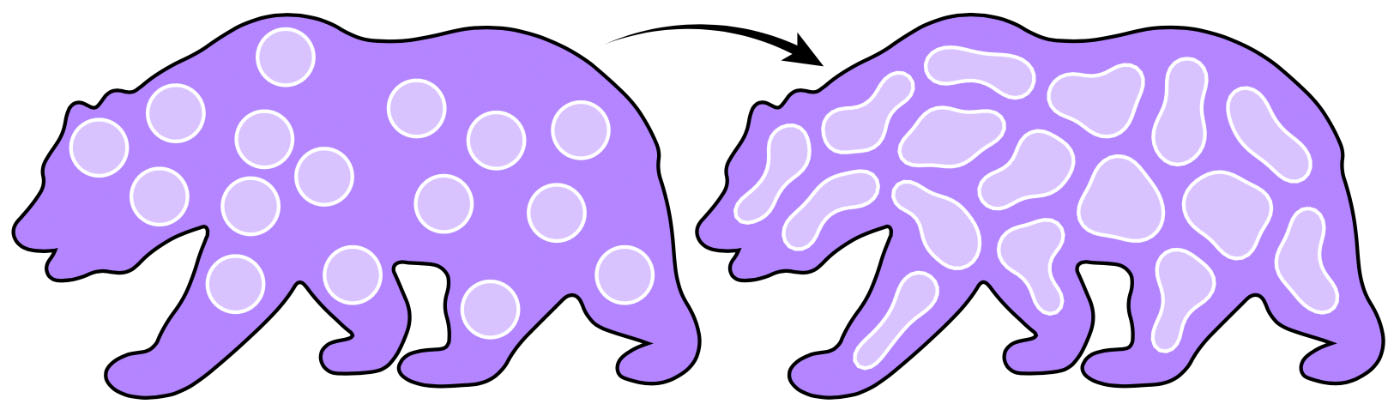
Assim como os potenciais repulsivos são usados para distribuir pontos igualmente, podemos calcular coleções de curvas igualmente espaçadas (aqui restritas a uma região por meio de um potencial de curva fixo).
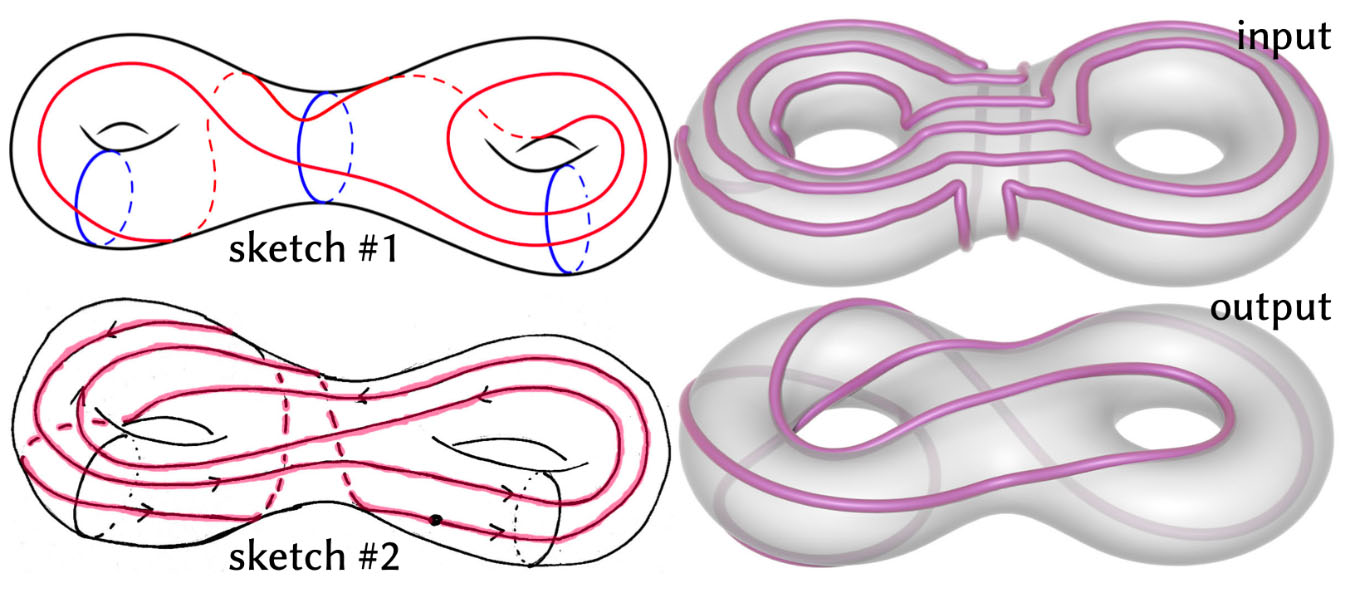
Loops topologicamente intrincados podem ser difíceis de desenhar à mão — os esboços à esquerda (desenhados por Nathan Dunfield) ilustram as coordenadas Dehn-Thurston . À direita, geramos uma versão equiespaçada desta curva ao fluir um esboço grosseiro, sujeito a uma restrição de superfície implícita.
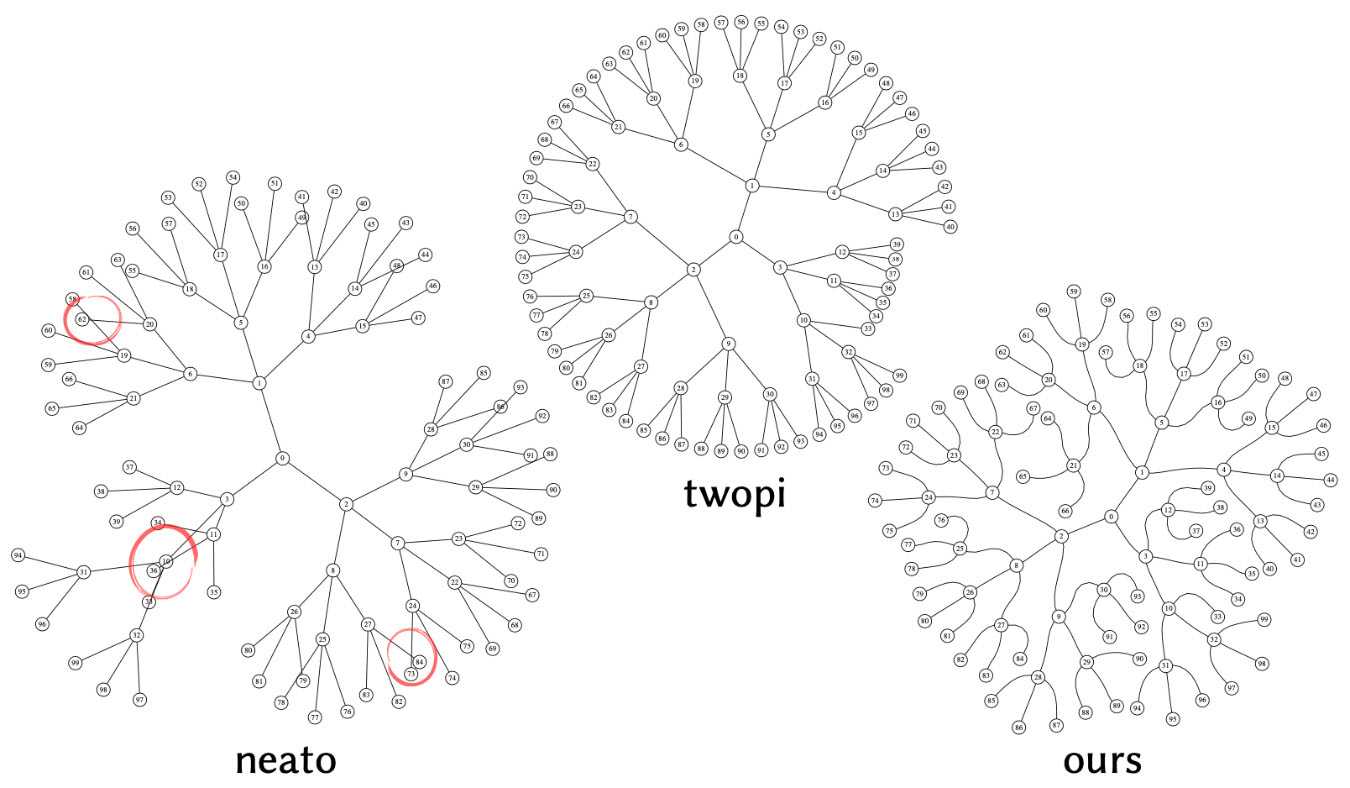
Algoritmos tradicionais de desenho de gráficos 2D baseados em proximidade nodal podem fazer com que as arestas se cruzem (esquerda) ou posicionem os nós extremamente próximos (centro) ; esses layouts foram produzidos pela popular biblioteca Graphviz . Ao tratar as arestas como curvas repulsivas, podemos obter desenhos gráficos que são mais compactos e mais legíveis (à direita) .
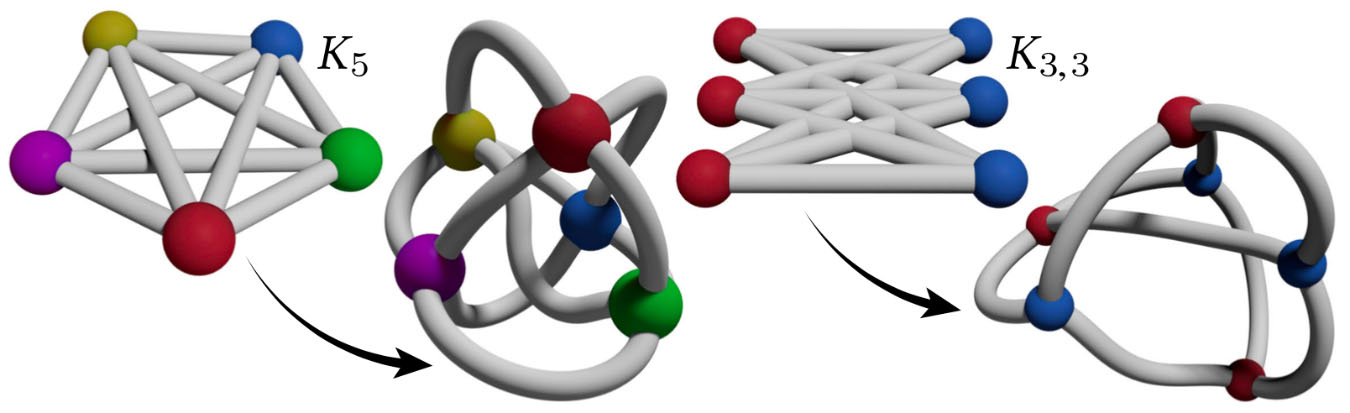
Incorporação isométrica: por desenhos 2D jitter de gráficos não planares (que necessariamente têm cruzamentos), a repulsão da curva com restrições de comprimento produz incorporações bem espaçadas em R 3 com comprimentos de borda prescritos.
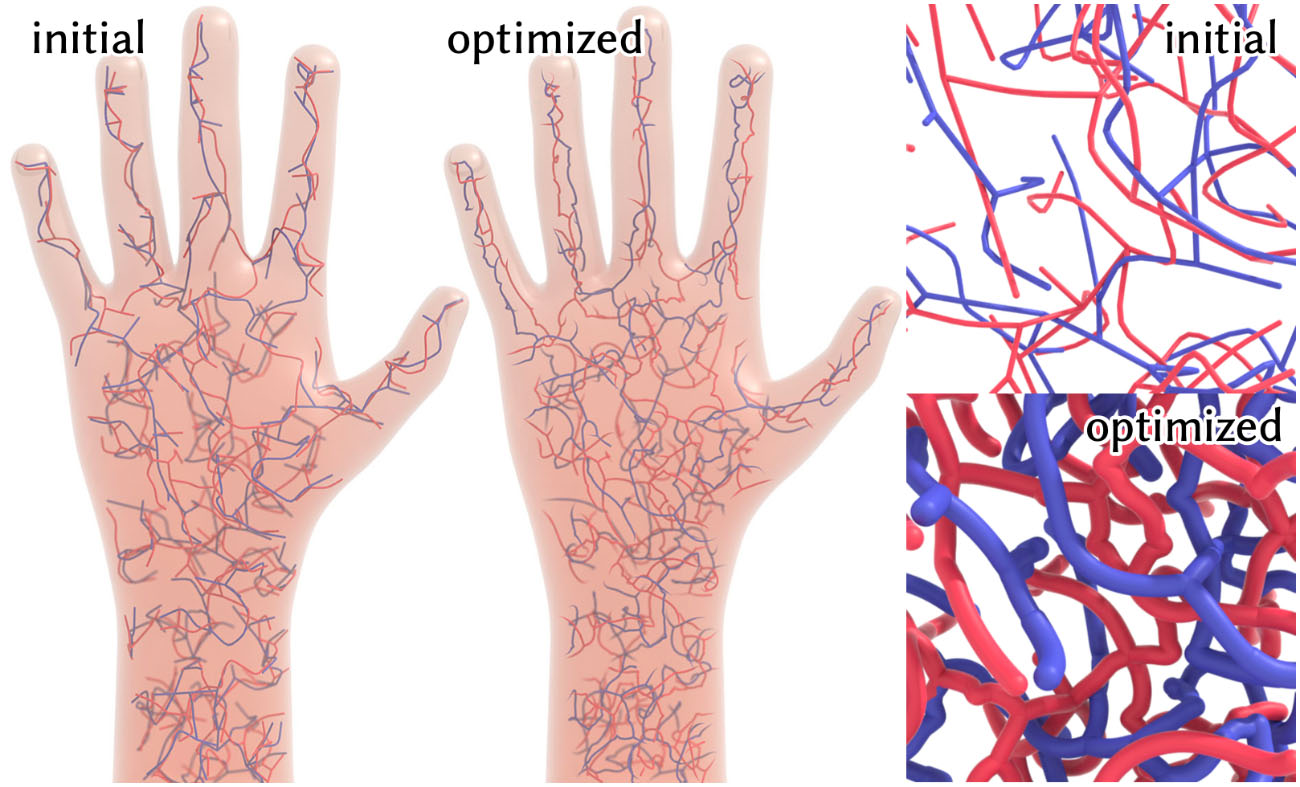
Esquerda: uma topologia inicial bruta para uma rede vascular sintética é otimizada para obter uma distribuição mais uniforme de nutrientes em um volume. Direita: plotar a espessura máxima sem colisões ajuda a visualizar a melhora na uniformidade.
Assim como nas curvas de Bézier, também podemos controlar as tangentes das curvas no interior e nas extremidades. Aqui fluímos uma curva poligonal (esquerda) , para uma interpolação suave com pontos fixos (vermelho) e pontos fixos e tangentes (azul) .
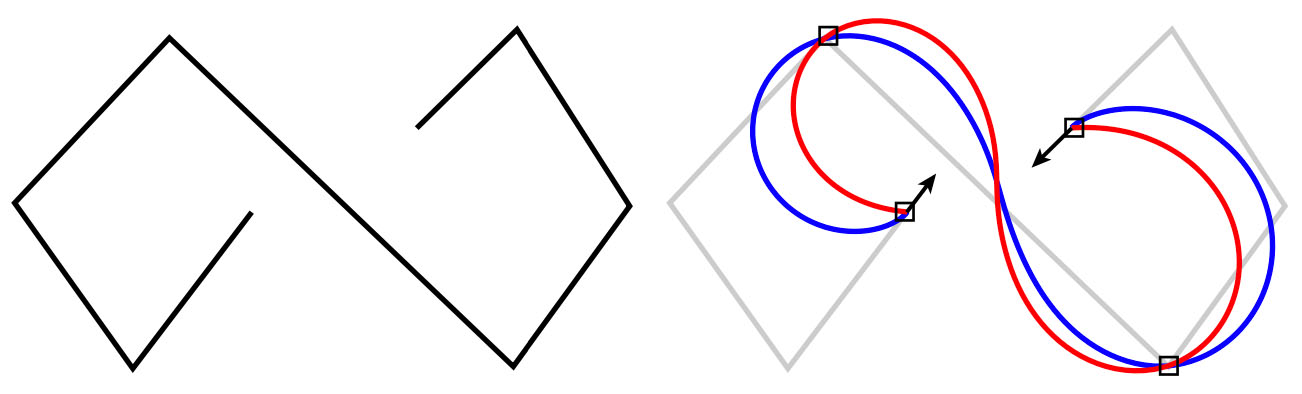
Os métodos de interpolação de curva padrão em programas de desenho 2D podem fazer com que as curvas se cruzem automaticamente (centro) , mesmo quando o polígono de controle (esquerda) não. Partindo do polígono de controle e restringindo os pontos de controle, obtemos um interpolante suave e sem interseção (direita) .
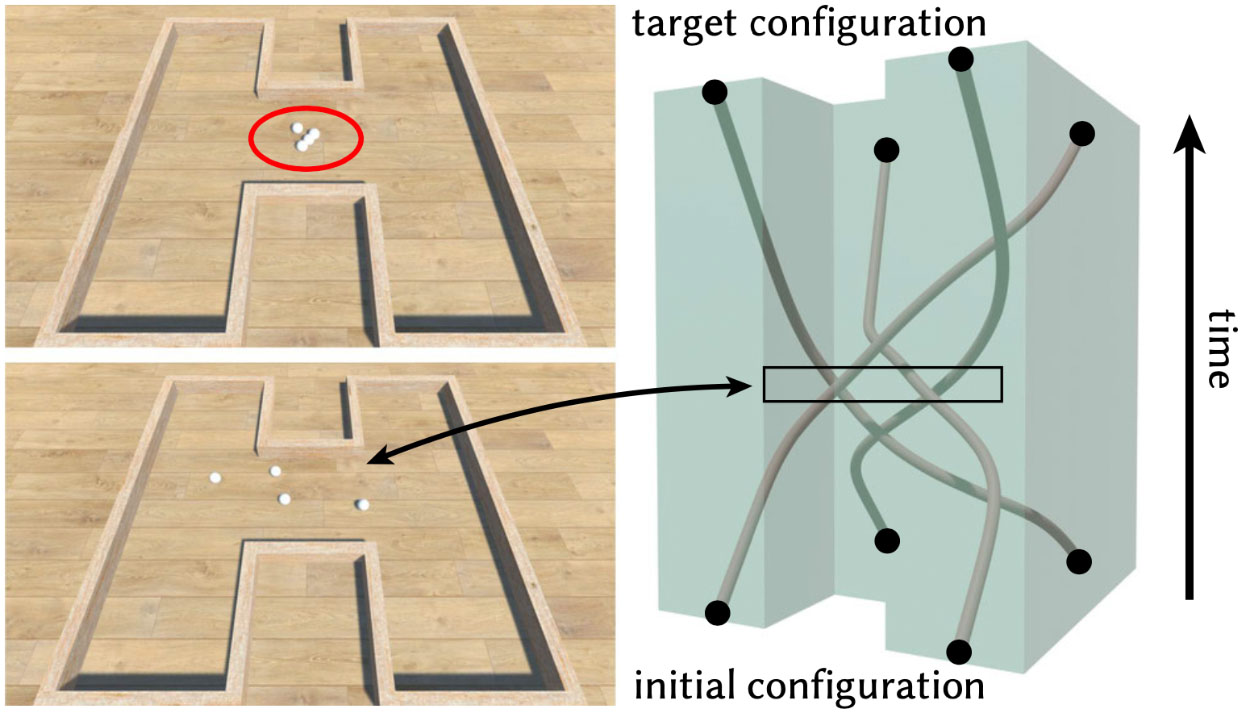
Canto superior esquerdo: neste cenário de planejamento de caminho, uma trajetória inicial aproxima os quatro agentes perigosamente. Inferior esquerdo: Ao tratar as trajetórias como curvas no espaço-tempo, nosso sistema fornece soluções que evitam ao máximo as colisões, tornando-as mais robustas para controlar erros. Direita: Encontrar trajetórias 2D é equivalente a otimizar uma trança 3D com extremidades fixas restritas a uma extrusão de um determinado ambiente. Essa mesma construção pode ser facilmente generalizada para ambientes 3D.
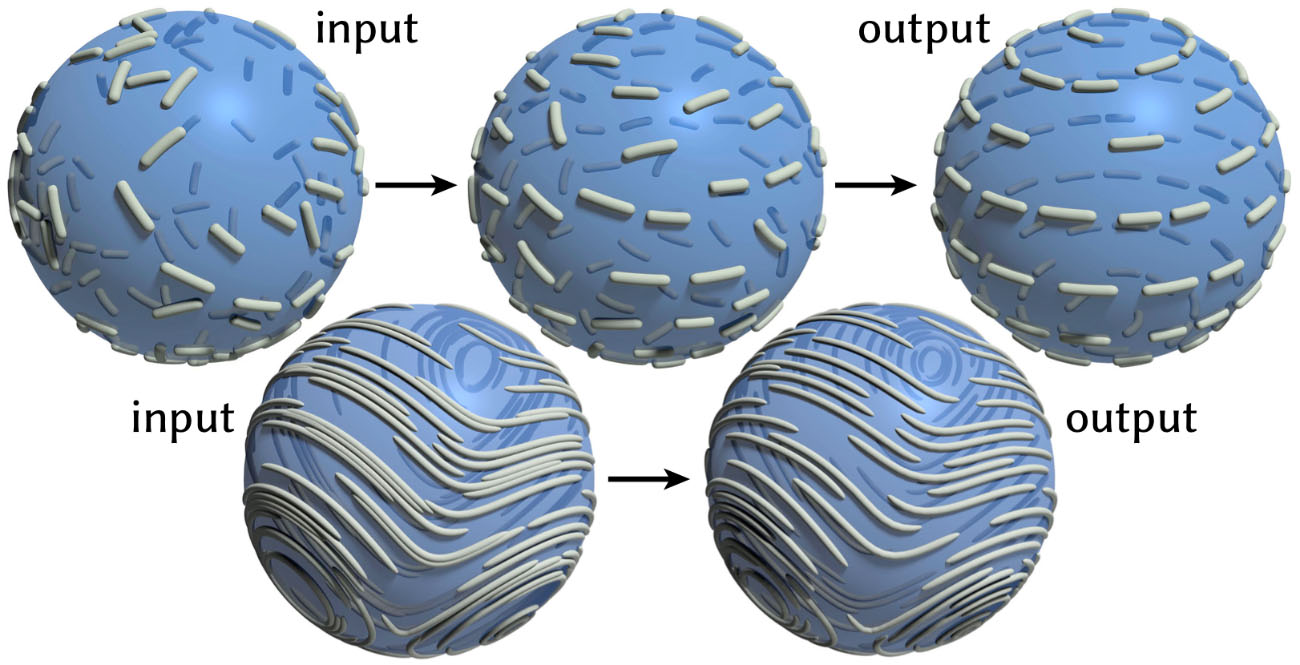
Incentivar as tangentes de curva a se alinharem com um determinado campo vetorial melhora a qualidade da visualização simplificada. Aqui, um conjunto aleatório de segmentos de curva (topo) se alinha com um campo vetorial rotacional; também podemos otimizar linhas de fluxo amostradas aleatoriamente (parte inferior) para melhorar seu espaçamento.

Desembaraçando um par de fones de ouvido via repulsão (veja o vídeo suplementar).
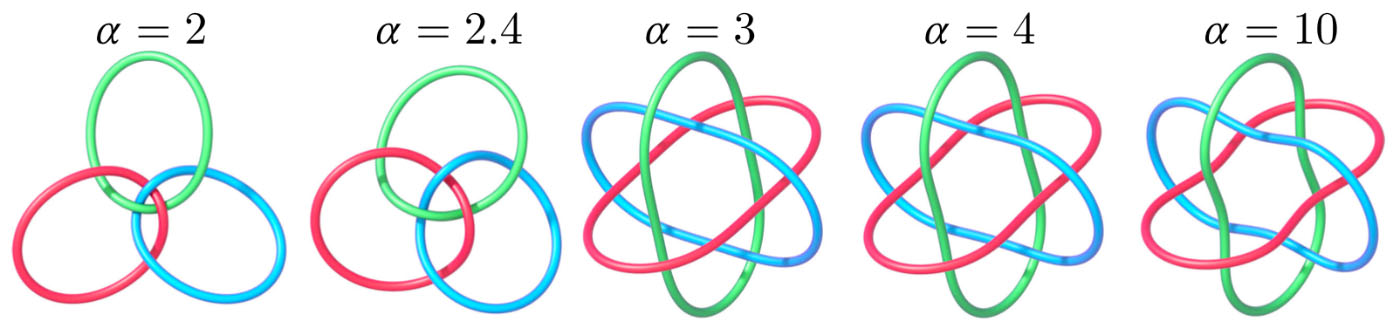
Minimizadores locais da energia do ponto tangente E 2α . Quando α = 2 a energia do ponto tangente é invariante em escala e pode apresentar “pontos apertados”; para valores maiores de α interações locais são mais penalizadas do que distantes.
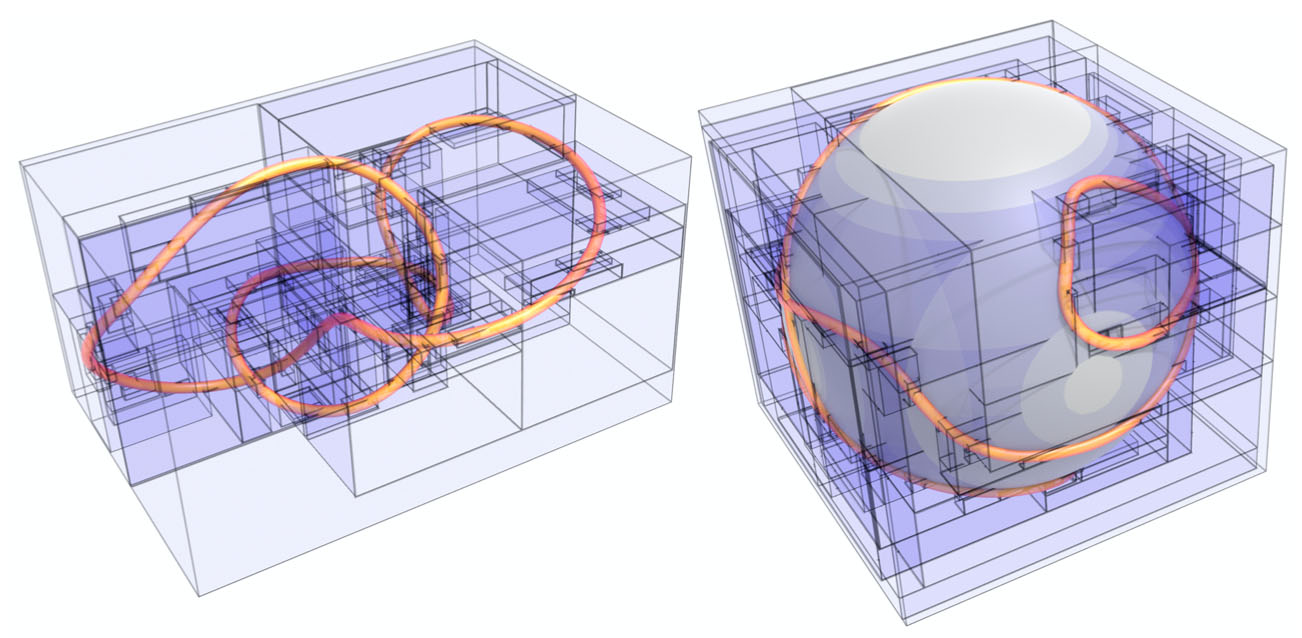
Para acelerar a avaliação da energia do ponto tangente, construímos uma hierarquia de volume delimitadora que divide ambas as posições (esquerda) e direções tangentes (direita) , aqui desenhadas como uma curva na esfera unitária.